 此文为《data abstraction and problem solving with c++》的读书笔记。这里有个图书管理系统模拟的应用实例
此文为《data abstraction and problem solving with c++》的读书笔记。这里有个图书管理系统模拟的应用实例
树中的每一个节点包含特定人员的数据。人名是查找关键字,是可在图中看到的唯一的数据项。下面的c++语句描述了树节点中的数据:
因为二叉查找树的本质上是递归的,所以很自然为树的操作设计递归算法。假设要在图1的二叉树中查找Ellen的记录。Jane在树的根节点中,所以若树中存在Ellen的记录,则必然在Jane的左子树中,因为按字母顺序,查找关键字Ellen在查找关键字Jane之前。有递归的定义知,Jane的左子树也是二叉树,因此可用完全相同的策略,在子树中查找ELlen。Bob是这个二叉查找树的根,因为关键字Ellen大于关键字Bob,所以Ellen的记录必然在Bob的右子树中。Bob的右子树也是二叉查找树,而Ellen正好在该树的叶节点中。这样就找到了Ellen的记录。
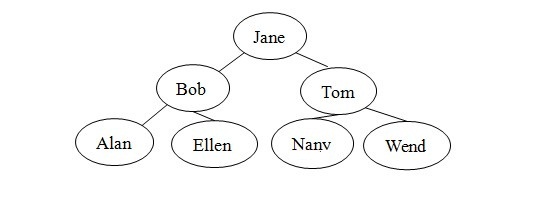
图1:二叉查找树
下面的伪码总结了查找策略:
后面将会看到,search算法是二叉查找树的插入、删除和检索操作的基础。
很多不同结构的二叉查找树可以包含人名Alan、Bob、Ellen、Jane、Nancy、Tom和Wendy。例如,除图1的树外,图2的每棵树都是人名的有效二叉查找树。虽然形状各不相同,但树的形状并不影响search算法的有效性。算法只要求树是二叉查找树。
对于search方法而言,一些树比另一些树的效率会更高。例如,在图2-c中,search算法在检查每个节点之后才找到Wendy,实际上,这个二叉查找树的结构与有序线性连接表相同,没有效率优势。而对于图1中的满二叉树,search算法只检查包含人名Jane、Tom和Wendy的节点。这些人名与图3中有序数组的折半查找将检查的人名相同。后面将进一步介绍二叉查找树的形状如何影响search的效率,以及插入和删除操作如何影响树的形状。
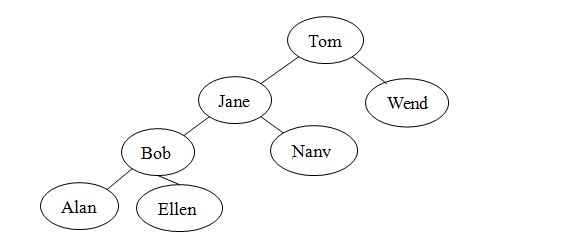
(a)
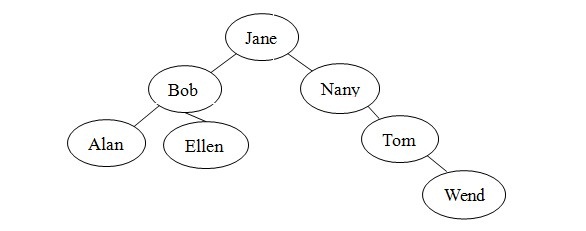
(b)

(c)
图2:与图1包含相同数据的二叉查找树
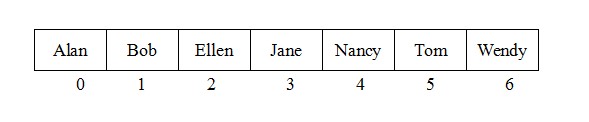
有序的人名数组
下面介绍的插入、删除、检索和遍历算法假设采用前面讨论的二叉树的基于指针的实现。稍作改动,即可将这些基本算法用于二叉树的其他实现。还假设节点项具有唯一查找关键字。
Insert
假设要将Frank的记录插入图1的二叉查找树中。第一步查找包含关键字Frank的项。search算法首先查找根为Jane的树,然后查找根为Bob的树,在查找根为Ellen的树。之后,查找以Ellen的右左孩子为根的树。如图3所示,因为树空,所以search算法到达基例,终止,并显示消息:不存在Frank。search在Ellen的右子树查找Frank意为着什么?首先,若Frank是ELlen的右孩子,则search将在那里找到Frank。
由这些观察可知,最好将Frank作为Ellen的右孩子插入。因为Ellen没有右孩子,所以插入很简单,只需要是Ellen的RightChild指针指向包含Frank的节点。更重要的是,Frank属于这个位置--search将在此处查找到Frank。更明确地讲,将Frank作为Ellen的右孩子插入将保持二叉查找树的属性。因为在查找Frank时,search将遵循到达Ellen的右孩子的路径,故可以确保:Frank与树中上部人名的关系正确。
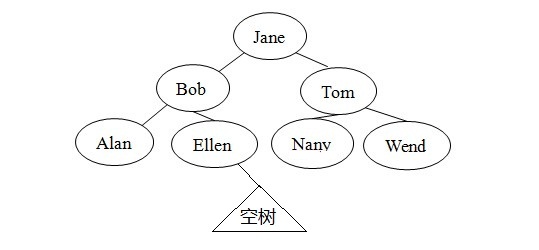
图3:search 算法在空子树终止
使用search来确定在树中哪个位置插入新人名称简化了插入操作。无论将哪个新项插入树中,search总在空树处终止,这样,search总是将记录作为新叶子插入。因为添加叶子只需要改双亲中的适当指针,所以插入需要的工作实际上与对应的查找是相同的。
下面的高级伪码描述了这个插入过程:
必须将节点parentNode的适当指针leftChildPtr 或rightChildPtr 设置为指向新的节点。后面将看到,若将treePtr传递为引用参数,则search算法的递归特性提供了设置指针的巧妙方法。于是将insertItem方法完善为:
该递归算法如何将leftChildPtr或rightChildPtr设置为指向新的节点呢?这与第四章介绍的有序链表的递归插入函数非常相似。若插入前树为空,则树的根的外部指针将为NULL,而且函数不会做递归调用。因为treePtr是引用参数,在它指向新节点时,实参,即树根的外部指针,也将指向新节点。图4-a显示在空树中插入(试想一下该递归的参数传递在C语言中是怎样实现的)。


(a) (b)
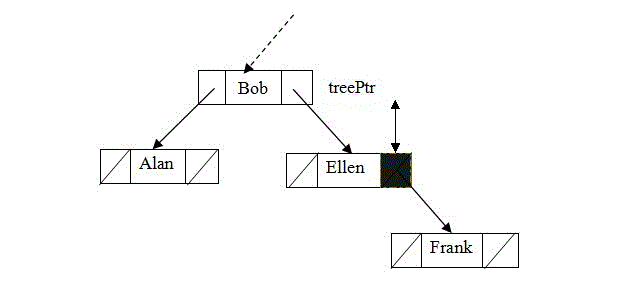
(c)
图4 (a)在空树中插入;(b)查找在叶子处终止;(c)在叶子处插入
insertItem的一般情况与空树的特例类似。当形参treePtr变成NULL时,对应的实参是空子树双亲中的leftChildPtr 或rightChildPtr指针,换言之,这个指针的值为NULL。通过一个递归调用,将该指针传给insertItem函数:
insertItem(treePtr->leftChildPtr,newitem);
或
insertItem(treePtr->rightChildPtr,newitem);
因此,当treePtr指向新节点时,形参,即双亲中的对应指针,就指向新的节点。图4中的b部分和c部分显示插入的一般情况。
可用insertItem构建二叉查找树。例如,从空树开始,若按次序插入Jane Bob Alan Ellen Tom Nancy 和Wendy,将得到如图1所示的二叉查找树。有趣的是,Jane Bob Alan Ellen Tom Nancy和Wendy正好是图1中树的先序遍历。也就是说,若取出二叉查找树的先序遍历的输出,并使用insertItem 构建二叉查找树,将得到一颗重复树。这没什么可以惊讶的,因为ADT二叉树的副本构造函数就是使用先序遍历复制树。
若按不同顺序插入前面的人名,则将得到一颗不同的二叉查找树。例如,按字母表顺序插入前面的姓名,将得到图2-c的二叉查找树。
delete
删除比插入要复杂些。首先用search算法来定位包含指定查找关键字的项,若找到,则必须从树中删除此项。算法的初始版本如下:
关键任务在于:
Remove item i from the tree
假设deleteItem在特殊节点N中找到项目i,分三种情况考虑:
(1)N是叶子
(2)N只有一个孩子
(3)N有两个孩子
第一种情况最容易处理。要删除包含元素i的叶子,只需要将其双亲的指针设置为NULL。
第二种情况比较更复杂;若N有一个孩子,则有两种可能性:
* N只有一个左孩子
* N中有一个右孩子
这两种可能性是对称的,因此,演示左孩子的解决方案就够了。在图5-a中,L是N的左孩子,而P是N的双亲。N可以是P的左孩子,也可以是P的右孩子。若树中删除节点N,L将没有双亲,P将去掉一个孩子。设使L替代N,作为P的一个孩子,如图5-b所示。这种方法保持了二叉查找树的属性吗?
例如,若N是P的左孩子,则以N为根的子树的查找关键字都小于P中的查找关键字。同样,以L为根的子树的所有查找关键字都小于P中的查找关键字。所以,再删除N,而且P收养了L后,P的左子树的所有查找关键字仍小于P中的查找关键字。因此,该删除策略保持了二叉查找树的属性。若N是P的右孩子,则方式类似。总之,在两种情况下,都保持了二叉查找树的属性。


图5:(a)N只有一个左孩子,N可以是P的左孩子也可以是P的右孩子; (b)删除节点N后
若要删除的项处在包含两个孩子的节点N中,则处理更困难,是三种可能中的最复杂的情况。
如图6所示。由上可知,当N只有一个孩子时,该孩子将替代N。而当N有两个孩子的情况下,不可能是两个孩子都替换N,N的双亲的空间有限,只能由N的一个孩子作为N的替代。很显然,需要一种不同的策略。

图6 :N有两个孩子
实际上,根本不必删除节点N。可找到另一个更易删除的节点,不删除N,而删除该节点。该策略似乎难以置信。但是,程序员编写下列语句
nameTree.searchTreeDelete(searchKey);
是期望从ADT二叉查找树中删除关键字等于searchKey的项。不过,编程者只希望删除该项,因为程序和ADT实现之间的墙,所以他们无权删除树中的节点。...//?
考虑另一种策略(怎样考虑到的??)。要从二叉查找树中删除包含两个孩子的节点N中的项,可采用下列步骤:
(1)在树中定位另一个节点M,M比N更容易删除。
(2)将M中的项复制到N,从而有效地从树中删除N的原始项。
(3)从树中删除节点M。
哪类节点M比节点N更容易删除?前面介绍了如何删除没有孩子或只含有一个孩子的节点,故可将此类节点用作M。但用小心,并不能随意在选择一个节点,将其数据复制到N,原因是必须将树的状态保持为二叉查找树。例如,在图7的树中,若将M的数据复制到N,则结果将不再是一个二叉查找树。
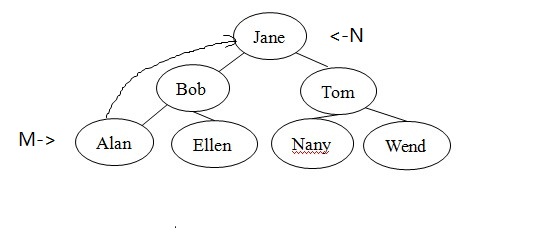
图7:并非任何节点都可用
究竟将哪个数据项复制到节点N,可以将树的状态保持为二叉查找树?N的左子树的所有查找关键字都小于N中的查找关键字,而N的右子树的所有查找关键字都大于N中的查找关键字。在用查找关键字y替换节点N中的查找关键字x时,必须保持这个属性。y值有两种可能性:按查找关键字的顺序,y可能紧接在x之前,也可以紧接在x之后。如果y紧接在x之后,则N的左子树的所有查找关键字都小于y,应为他们都小于x,如图8所示。而N的右子树的所有查找关键字都大于等于y,因为它们大于x,而且根据假设,该树不存在介于x和y之间的查找关键字。若按查找关键字的顺序,y紧接在x之前,则y大于等于N的左子树的所有查找关键字,而小于N的右子树的所有查找关键字。
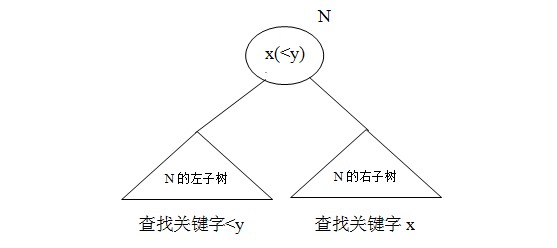
图8:可用y代替查找关键字x
因此,可将查找关键字紧接在N的查找关键字之后的项复制到N,也可以将查找关键字紧接在N的查找关键字之前的项复制到N 。假设要使用查找关键字y 紧接在N的查找关键字之后的节点。这个查找关键字称为x的中序后继(inorder successor)。如何定位该节点?因为N有两个孩子,所以查找关键字的中序后继是N的右子树的最左侧节点。换言之,要查找包含y的节点,可以跟踪指向N的右孩子R的rightChild指针(这一定存在,因为N有两个孩子)。然后沿以R为根的树向下,采用各个节点的左分枝,直到遇到没有左孩子的节点M为止。将节点M的项复制到N,M没有左孩子,故可用两种简单情况之一从树中删除M。如图9所示。
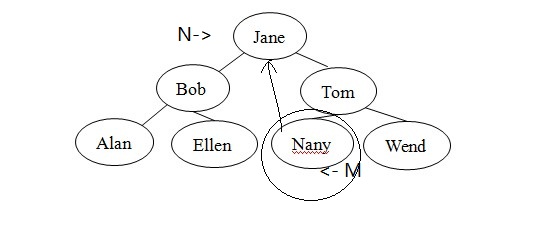
图9:M的查找关键字是N的查找关键字的中序后继,将M的数据项复制到N
下面是更详细的删除算法的高级描述:
在下面的完善代码中,采用了search的算法,并将其直接插入到deleteItem。另外,函数deleteNodeItem 使用ProcessLeftMost函数查找节点M中的项。即节点N的中序后继。函数processLeftMost返回M的项,此后,从树中删除M。然后用返回的项替换节点N中的项,从而将其从二叉查找树中删除。
与insertItem函数一样,与treePtr对应的实参要么是N的双亲的指针之一,如图10所示,要么是根的外部指针(此时,N是原始树的根)。无论哪种情况,treePtr都指向N。这样若通过实参treePtr调用deleteNodeItem函数更改treePtr,则将更改Nde双亲的指针。若N有两个孩子,deleteNodeItem将调用递归函数processLeftMost ,使用相同的策略,删除包含待删除项的节点的中序后继。
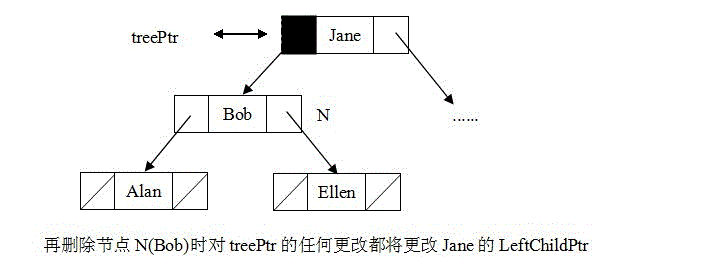
图10:节点N的递归删除
retrieve
通过完善search算法,可实现检索操作。search算法的代码如下:
如果存在需要的查找关键字,则检索操作必须返回包含该关键字的项。否则,必须抛出异常TreeException 所以,检索的算法如下:
traverse
二叉查找树与二叉树的遍历相同,但要认识到,二叉查找树的中序遍历将按有序的查找关键字的顺序访问树的节点。在证明此陈述前,先回顾一下中序遍历算法:
定理二:叉查找树T的中序遍历将按有序的查找关键字的顺序访问节点。
证明 此证明在T的高度h上归纳。
基例:h=0。当树空时,算法不访问任何节点。对于树中人名为零的情况,这当然是有序的。
归纳假设:假设对所有k,0<k<h,这定理成。换言之,对于所有k(0<k<h),中序遍历按有序的查找关键字顺序访问节点。
归纳结论:必须说明,对于k=h>0,该定理成立。T的形式为:
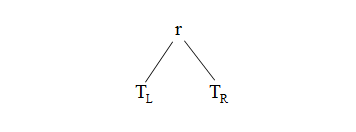
因为T是二叉查找树,所以左子树TL中的所有查找关键字都小于根r的查找关键字,而右子树TR中的所有关键字都大于根r的查找关键字。inorder算法将访问TL中的所有节点,然后访问r,在访问TR中的所有节点。所以,唯一考虑的是inorder按正确顺序访问TL和TR子树的各个节点。但是因为T是高为h的二叉查找树,所以两棵树都是高度小于h的二叉查找树。按照归纳假设,inorder将按正确的有序关键字的顺序访问TL和TR子树的节点。证毕。
由此定理知:inorder在访问节点后立即访问节点的中序后继。
分享到:





 此文为《data abstraction and problem solving with c++》的读书笔记。这里有个
此文为《data abstraction and problem solving with c++》的读书笔记。这里有个



















相关推荐
二叉搜索树(BST,Binary Search Tree)又称二叉查找树或二叉排序树。 一棵二叉搜索树是以二叉树来组织的,可以使用一个链表数据结构来表示,其中每一个结点就是一个对象。 一般地,除了key和位置数据之外,每个结点...
c++ 二分搜索树 二分查找树 binary search tree BST
二分搜索树(英语:Binary Search Tree),也称为 二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。满足以下几个条件: 若它的左子树不为空,左子树上所有节点的值都小于它的根节点。 若它的右子树不为空,右子...
用C#实现的二叉查找树的算法,实现了算法。
binary search tree 二叉搜索树的C++实现,有插入、删除、查找、查找最大最小等功能,并附有测试例子,简单易懂
是Binary Search Tree code 二叉检索树的代码,实现了插入,删除,检索,遍历,包括先序遍历,中序遍历,后序遍历
关于最优二叉查找树的开山之作,介绍了最优二叉查找树的概念,以及构造最优二叉查找树的动态规划算法,来自D. E. KNUTH,发表于1971年,亦可从这里下载:...
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties: The left subtree of a node contains only nodes with keys less than the node's key. The right ...
本文实例讲述了JS中的算法与数据结构之二叉查找树(Binary Sort Tree)。分享给大家供大家参考,具体如下: 二叉查找树(Binary Sort Tree) 我们之前所学到的列表,栈等都是一种线性的数据结构,今天我们将学习...
二叉搜索树,包括插入、删除、查找、显示等功能
二叉排序树(Binary Sorting Tree)又称二叉搜索树(Binary Search Tree),是一种特殊结构的二叉数,作为一种排序和查找的手段,对应有序表的对半查找,通常亦被称为数表。其定义也是递归的。 二叉排序树的定义:...
二叉排序树(Binary Search Tree,BST)是一种特殊的二叉树,它具有以下特点: 每个节点最多有两个子节点,分别称为左子节点和右子节点。 对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,而右子树...
二叉排序树(Binary Search Tree,BST)是一种特殊的二叉树,它具有以下特点: 每个结点最多有两个子结点,称为左子结点和右子结点。 对于树中的每个结点,其左子树中的所有结点的值都小于该结点的值,而右子树中的...
avl树的插入删除操作,并包括判断输入的二叉查找树是否为avl树,以及把二叉查找树转换为avl树
二叉排序树(又称二叉查找树):(1)若左子树不空,则左子树上所有节点的值均小于它的根结点的值;(2)若右子树不空,则右子树上所有节点均大于它的根结点的值;(3)它的左右子树分别为二叉排序树。 二叉平衡树:若...
Binary Search Tree 利用C++實現 Binary Search Tree
最小成本二分检索树optimal binary optimal binary
二叉排序树(Binary Sort Tree)又称二叉查找(搜索)树(Binary Search Tree)。其定义为:二叉排序树或者是空树,或者是满足如下性质的二叉树:1.若它的左子树非空,则左子树上所有结点的值均小于根结点的值;2.若它的右...
针对二叉搜索树的编程接口,包括如下接口: 初始化为空树 判断树是否为空 判断树是否已满 确定树中节点个数 向树中添加一个节点 判断树中是否存在某个节点 从树中删除一个节点 将某个函数作用于树中每个节点 删除树...